Función Cuadrática

Las funciones comparten nuestra vida cotidiana más a menudo de lo que seguramente creemos. Las hay de todo tipo, según correspondan o no a una generalización.
En muchos casos resulta conveniente representar varias funciones en un mismo grafico, permitiendo de este modo efectuar un estudio comparativo de las mismas. Por medio de ellos, el dueño de una empresa puede evaluar el rendimiento de la misma; un físico puede establecer el tipo de movimiento de un planeta, y un químico, la acidez de un liquido. Por otra parte, muchos de los fenómenos naturales que nos rodean están sujetos a un cambio continuo. Por ejemplo, una planta crece a medida que el tiempo transcurre, puede detener su crecimiento en algún instante, para luego volver a crecer, o permanecer estacionaria. O bien, la población de un país, que varia con el correr de los años, según la cantidad de muertes y nacimientos.
En todos los ejemplos presentados se producen cambios en los cuales una variable depende de otra. Es importante “medir” estas variaciones y expresarlas en números.
Por ejemplo, las funciones cuadráticas son utilizadas en algunas disciplinas como, por ejemplo, Física y Economía. Son útiles para describir movimientos con aceleración constante, trayectorias de proyectiles, ganancias y costos de empresas, y obtener así información sin necesidad de recurrir a la experimentación.

Definición:

Función polinómica de segundo grado. f(x) = a.x² + bx + c siendo a, b, c números reales y a≠0

La representación gráfica es una PARÁBOLA.

-->>Distintas situaciones que se pueden presentar: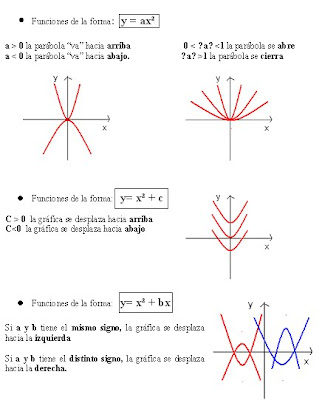 Elementos de una parábola:

• Raíces de la parábola: son los puntos de intersección de la gráfica y el eje x, vale decir que f(x)=0.

Se pueden dar tres casos, siendo ∆ = b² - 4.a.c (discriminante)

Si ∆ > 0 Raíces reales distintas

Si ∆ = 0 Raíces reales iguales

Si ^ = 0 Raíces no reales

• Vértice de la parábola:
• Eje de simetría: es la recta que tiene por ecuación x = xv

• Ordenada al origen: es el punto de intersección de la gráfica con el eje y, vale decir que f(0) = c

-->> La función cuadrática puede ser expresada de distintas maneras: